aufgaben in rot sind noch in bearbeitung

endergebnisse hebe ich oft in dieser farbe hervor

anleitung zu online aufgabe 1

ln( a · x^2 + b · y^2 + c · z^2 ) nach x ableiten   › › ›   term eins = 2a · x / ( a · x^2 + b · y^2 + c · z^2 )

ln( a · x^2 + b · y^2 + c · z^2 ) nach y ableiten   › › ›   term zwei = 2b · y / ( a · x^2 + b · y^2 + c · z^2 )

ln( a · x^2 + b · y^2 + c · z^2 ) nach z ableiten   › › ›   term drei = 2c · z / ( a · x^2 + b · y^2 + c · z^2 )

zahl eins , zahl zwei , zahl drei aus  a = ( zahl eins , zahl zwei , zahl drei ) für x , y , z  in term eins , term zwei , term drei einsetzen   › › ›   neuzahl eins , neuzahl zwei , neuzahl drei

neuzahl eins · zahl vier + neuzahl zwei · zahl fünf + neuzahl drei · zahl sechs ist die lösung

hierbei v = ( zahl vier , zahl fünf , zahl sechs )

anleitung zu online aufgabe 2

H 93 a

ich fasse im folgenden M_1 als teilmenge von R (der menge der reellen zahlen) auf

die menge M_1 verfügt über keine inneren punkte – die menge der inneren punkte ist somit leer

der rand und auch der abschluss von M_1 ist M_1 ›vereinigt mit‹ der 1-elementigen menge {0}

H 93 b

H 93 c

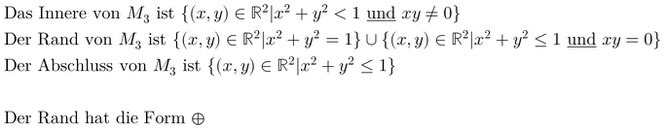
H 93 d

das innere von M_4 ist das innere der ›einheitskugel‹ (mit mittelpunkt (0,0,0) und radius 1) ohne die menge der in der x-y-ebene liegenden punkte

der rand besteht aus der oberfläche der ›einheitskugel‹ ›vereinigt mit‹ dem inneren des in der x-y-ebene liegenden ›einheitskreises‹ ›vereinigt mit‹ jenem teil der z-achse, welcher nicht teil der ›einheitskugel‹ ist

der abschluss von M_4 ist die gesamte ›einheitskugel‹ (samt rand) ›vereinigt mit‹ der z-achse

H 94 a b c

(ich schreibe – wie auch bisher – die argumente x und y nebeneinander und nicht übereinander)

H 94 b

siehe oben

H 94 c

siehe oben

H 95 a

f ( 2 , –1 , 0 ) = 3

f_x ( 2 , –1 , 0 ) = –2

f_y ( 2 , –1 , 0 ) = 0

f_z ( 2 , –1 , 0 ) = 4

f_xx ( 2 , –1 , 0 ) = 0

f_xy ( 2 , –1 , 0 ) = 0

f_xz ( 2 , –1 , 0 ) = 9

f_yx ( 2 , –1 , 0 ) = f_xy ( 2 , –1 , 0 )

f_yy ( 2 , –1 , 0 ) = 6

f_yz ( 2 , –1 , 0 ) = 0

f_zx ( 2 , –1 , 0 ) = f_xz ( 2 , –1 , 0 )

f_zy ( 2 , –1 , 0 ) = f_yz ( 2 , –1 , 0 )

f_zz ( 2 , –1 , 0 ) = 0

Hf ( 2 , –1 , 0 ) =   0    0    9

Hf ( 2 , –1 , 0 ) =   0    6    0

Hf ( 2 , –1 , 0 ) =   9    0    0

H 95 b

T_2 ( f , ( x , y , z ) , ( 2 , –1 , 0 ) ) = 3 – 2( x – 2 ) + 4z + 9( x – 2 )z + 3( y + 1 )^2

T_1 ( f , ( x , y , z ) , ( 2 , –1 , 0 ) ) = 3 – 2( x – 2 ) + 4z + 9( x – 2 )z + 3( y + 1 )^2

T_0 ( f , ( x , y , z ) , ( 2 , –1 , 0 ) ) = 3 – 2( x – 2 ) + 4z + 9( x – 2 )z + 3( y + 1 )^2

H 95 c

g ( x , y , z ) = T_1 ( f , ( x , y , z ) , ( 2 , –1 , 0 ) ) + term eins

h ( x , y , z ) = T_1 ( f , ( x , y , z ) , ( 2 , –1 , 0 ) ) + term zwei

term eins und term zwei könnten beide zum beispiel von folgender form sein

a · ( x – 2 ) · ( x – 2 )  + b · ( y + 1 ) · ( y + 1 ) + c · ( z – 0 ) · ( z – 0 ) +

d · ( x – 2 ) · ( y + 1 ) + e · ( x – 2 ) · ( z – 0 ) + f · ( y + 1 ) · ( z – 0 )

oder kürzer

a ( x – 2 )^2  + b ( y + 1 )^2 + c z^2 + d ( x – 2 ) ( y + 1 ) + e ( x – 2 ) z + f ( y + 1 ) z

H 96 a

H 96 b

H 96 c

H 96 d