aus diversen gründen kann ich die crashkurse nicht wie geplant stattfinden lassen
ich versuche alternativlösungen zu finden [stand 07. dezember 2022]
sobald mir dies gelungen ist, wird an dieser stelle ein anmeldeformular erscheinen
– – –
die termine der crashkurse für die vorbereitung auf die erste scheinklausur HM 1 2022 sind
26. november* 03. dezember* 10. dezember*
jeweils 12 bis 17 uhr
– – –
*findet nicht statt
diese seite wird gerade aufgeräumt
deshalb kann (vorübergehend) ein chA _oti.scher eindruck entstehen)
NEU
NEU
gaaanz unten auf dieser seite sind (für HM2) einige auch für 2018 brauchbare links und beantwortete fragen aus 2016 zu finden
die bei ›LGS‹ verwendeten abkürzungen K und W stehen für KÜRZEN und WUSELN ... letzteres ist ein nervenschonender und zeitsparender ersatz für das gauß-verfahren und wird im rahmen des crashkurses genau erläutert ... auch die weiter unten aufrufbare datei ›wuseln‹ versteht sich als anleitung für dieses verfahren
D R E H U N G / S P I E G E L U N G

D I A G O N A L I S I E R B A R K E I T

whatsapp FRAGEN und ANTWORTEN
aktuell EINS bis ZWÖLF
fortsetzung von ANTWORT ELF

FRAGE EINS
Hallo Andreas ich versteh nicht wie ich bei dieser Aufgabe überhaupt starten soll
2009 10

ANTWORT EINS

FRAGE ZWEI

ANTWORT ZWEI

FRAGE DREI

ANTWORT DREI



FRAGE FÜNF
Wie löst man 2016 5b ?
ANTWORT FÜNF a

FRAGE SECHS
Hi [...] wie funktioniert diese Quadrik? Wir kommen nicht auf die Normalform. Vermutlich klappt etwas nicht bei der Quadratischen Ergänzung.

ANTWORT SECHS

FRAGE SIEBEN
2008 3 1

ANTWORT SIEBEN

FRAGE ACHT
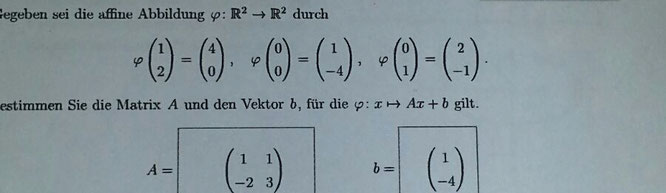
Ich komme einfach nicht auf diese Lösung und beiße mir die Zähne aus.
Könntest du mir sagen wie der rechenweg aussieht?
ANTWORT ACHT

FRAGE NEUN
[...] kann der Nullvektor ein Eigenvektor einer Matrix sein und kann eine Matrix den Eigenwert 0 haben?
ANTWORT NEUN
die sache ist ähnlich einzuordnen, wie das verhältnis der 1 zu den primzahlen ... ebenso wie die 1 nicht zu den primzahlen gezählt wird (obgleich sie doch außer sich selbst und 1 keine weiteren teiler besitzt), rechnet man den nullvektor gemeinhin nicht zu den eigenvektoren, obwohl jede (von der größenordnung her passende) matrix multipliziert mit dem nullvektor ein (wenn auch ziemlich unbestimmtes) vielfaches des nullvektors ergibt – mithin also die definition eigenvektor eigentlich erfüllt ist
dennoch – um die verwirrung komplett zu machen – enthält jeder eigenRAUM den nullvektor
der eigenWERT 0 ist von solcher spitzfindigkeit hingegen nicht betroffen – ein eigenWERT 0 ist möglich (und kommt im zusammenhang mit der zweiten scheinklausur auch mehr als ein mal vor)
CRASHKURS HM2 2016 (BEENDET)
LAGRANGE › 2008 8
PARAMETRISIERUNG › 2014 6 › 2015 9
POTENTIAL › 2008 5 › 2014 6
quadratische approximation – TAYLORPOLYNOM zweiter stufe › 2008 4
STETIGKEIT – epsilon delta › 2013 7
DIFFERENZIERBARKEIT › 2015 4