QUADRIKEN

hier sind umfangreiche aufräumarbeiten im gang

stand 07. august 2019

euklidische normalformen – affine klassifikationen

dies ist meine private gedächtnisstütze – bitte mit vorsicht genießen!

DIVERSE RECHENSCHNIPSEL

umwandlung in euklidische normalform ohne notwendigkeit einer transformationsmatrix F

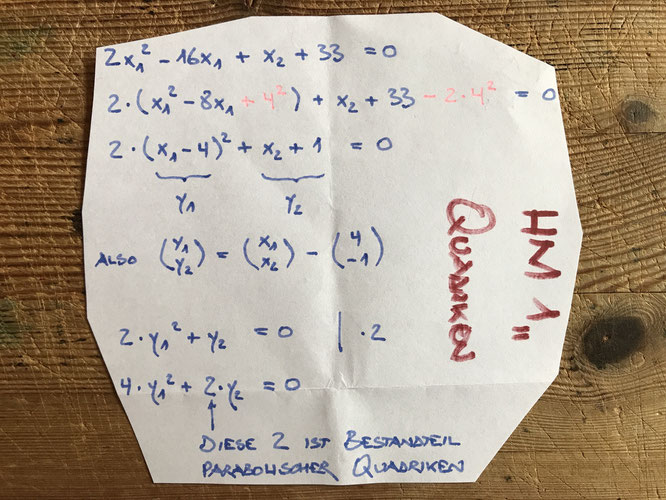
parabolische quadrik

eine nach unten geöffnete parabel mit scheitelpunkt ( 4 , –1 )

umwandlung in euklidische normalform

in der viertletzten zeile fehlt hinter 2/√2 ein y_1

kegelige quadrik

die zielmarke wäre auch mit 2 · (z_1)^2 – 2 · (z_2)^2 = 0 und (z_1)^2 – (z_2)^2 = 0 erreicht

alle drei gleichungen beschreiben zwei sich im punkt ( –1 , 2 ) schneidende geraden

 diese geraden verlaufen parallel zu den koordinatenachsen des x_1 – x_2 – koordinatensystems

( –1 , 2 ) ist der ursprung des z_1 – z_2 – koordinatensystems

das y_1 – y_2 – koordinatensystem und das z_1 – z_2 – koordinatensystem sind rechtssysteme

ALLERLEI FRAGEN – ALLERLEI ANTWORTEN

zu 2016 5 1

Sind die drei identisch? Spielt also die Reihenfolge der EV in einer Orthogonalmatrix eine Rolle?

Ist bei der euklidischen Normalform die Reihenfolge der EW egal??

weder die reihenfolge der eigenwerte, noch die der (normierten) eigenvektoren spielt bei der bestimmung der euklidischen normalform eine rolle – es ist lediglich darauf zu achten, dass die einmal gewählte reihenfolge konsequent beibehalten wird ... die solchermaßen entstehenden transformationsmatrizen sind zwar nicht identisch, führen aber allesamt zu einem korrekten ergebnis, welches auch von dem in der musterlösung angegebenen abweichen darf